2023. 9. 15. 22:47ㆍGoogle ML Bootcamp/4. Convolutional Neural Networks
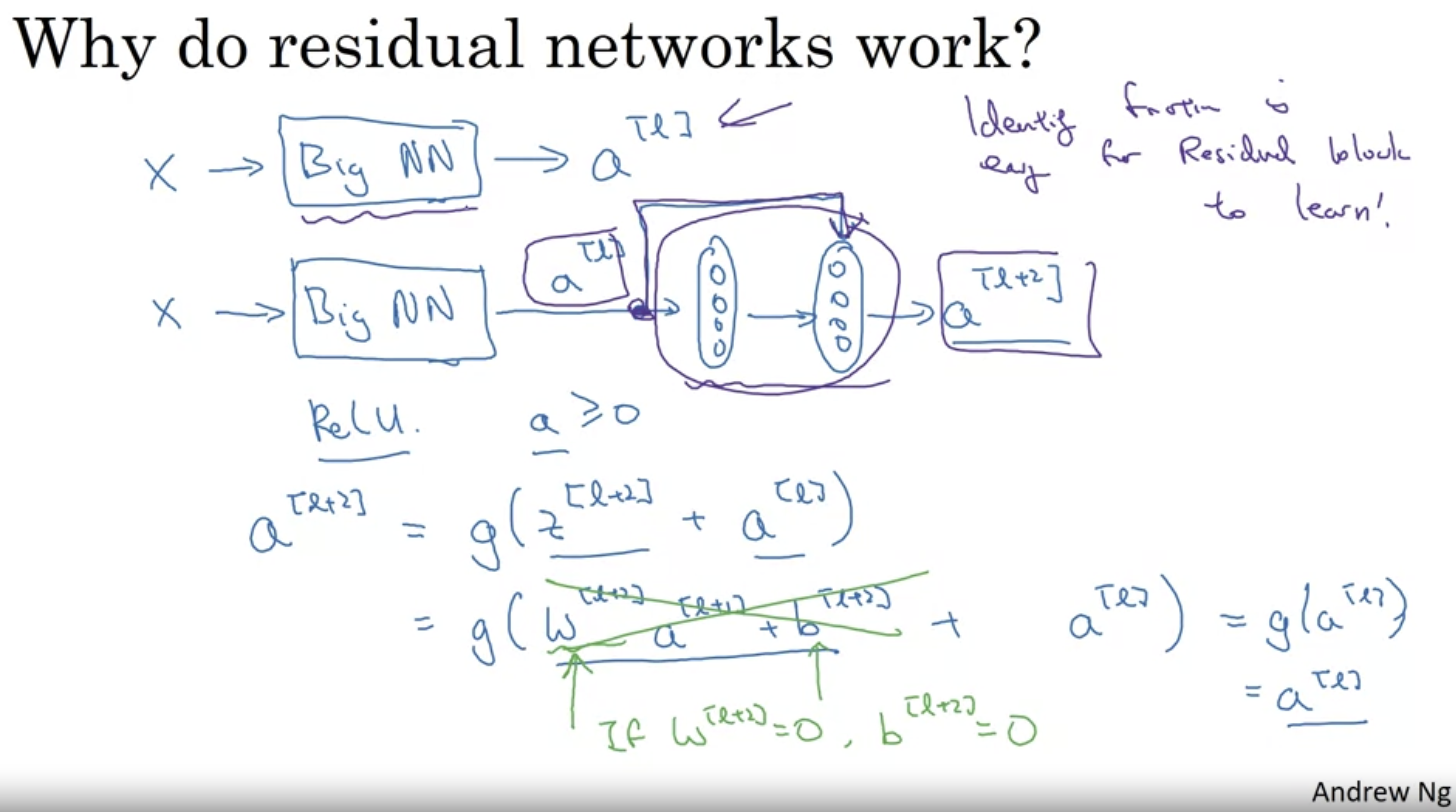
activation function : ReLU라고 가정했을 때 모든 A >= 0 이다.
if L2와 같은 Regularization을 통하면 W[l+2]가 감소하는 경향이 있다.
- W[l+2] = 0 까지 감소했다고 한다면 A[l+2] = A[l] 임을 볼 수 있다.
- 만약 residual block이 없었다면 해당 값은 0으로 전해지고, ReLU를 통해 계속 0으로 전달되므로 사실 이후의 깊이에서는 하는게 없는거나 다름없다. 오히려 나쁘게 만들 수도 있다.
- residual block이 존재함으로써 0이 아닌 값이 전달될 수 있고, 따라서 학습에 도움이 된다.
- 적어도 항등함수임을 학습하는 parameter를 쉽게 정할 수 있도록 도와준다.
residual block은 모델의 중간이나 끝, 어디에 추가하더라도 적어도 수행능력을 저하시키지는 않는다.
residual network에서는 same convolution을 사용하기 때문에 A[l+2].shape와 A[l].shape이 같다.
- if no padding convolution을 사용할 경우, residual block에서 A[l]을 추가하는 거 대신 np.dot(W(s),A[l])을 추가하면 된다.
- W(s)는 parameter일수도, 그냥 상수 일수도 있다.
'Google ML Bootcamp > 4. Convolutional Neural Networks' 카테고리의 다른 글
| 17. Inception Network Motivation (0) | 2023.09.15 |
|---|---|
| 16. Networks in Networks and 1x1 Convolutions. (0) | 2023.09.15 |
| 14. ResNets (0) | 2023.09.15 |
| 13. Classic Networks (0) | 2023.09.15 |
| 12. Why look at case studies? (0) | 2023.09.15 |