2023. 1. 27. 13:15ㆍAI수학/Linear Algebra(선형대수학)
이전 글에서는 matrix 개념, matrix를 Systems of linear algebraic equations에서 사용하는 이유를 알아보았다.
이제 AX=B 가 무엇을 의미하는지 안다고 생각한다.
결국 우리는 해를 구하기 위해 방정식을 세우는 것인데, 그렇다면 해는 어떻게 구하나?
그때 solution이 가우스 소거법(Gaussian elimination)이다.
가우스 소거법: AX=B 를 UX=C로 치환한다. 이때 U는 Upper triangle matrix의 약자이다.
- 법칙 1: Ri 와 Rj는 서로 interchange 가능 (R은 Row를 의미. 아래첨자는 i-th, j-th를 의미.)
- 법칙 2: Ri = a*Ri + b*Rj (단 a != 0)
쉽게 말하면 연립방정식 풀때 한 수식을 양변에 상수배만큼 곱하여 다른 식과 소거하여 변수의 개수를 줄이는 방법과 동일한 것이다.
예시로 쉽게 확인해보자. AX=B 를 다음과 같이 표시했다고 가정하자.




1.
R2 <- R2 - R1
R3 <- R3-2R1
를 수행.
2.R2 와 R4 interchange (Upper triangle matrix를 만들기 위함)

3. Upper triangle matrix를 위해 R32=0이 되어야 한다.
- R3 <- R3 + 3R2

4. interchange할 필요는 없다.
5. Upper triangle matrix를 위해 R43=0이 되어야 한다.
UX=C 치환 완료. 이를 x,y,z,w 변수로 다시 표현해보자.

계산을 해보면 x=9/19, y=131/19, z=33/19, w=-12/19 이렇게 구할 수 있을 것이다.
다음과 같이 여러 변수가 존재하는 연립방정식을 푸는 방법으로 가우스 소거법을 알아보았다.
직접 해보기에는 일일이 변수 소거법을 통해 하나씩 찾아가는 방법보다는 조금? 간단한 것 같았다.
하지만 중요한거는 컴퓨터가 하기 편한 방법을 찾아주어야 한다는것..이는 매우 효과적인 방법이라고 한다.
++ if inconsistent system(=equation)
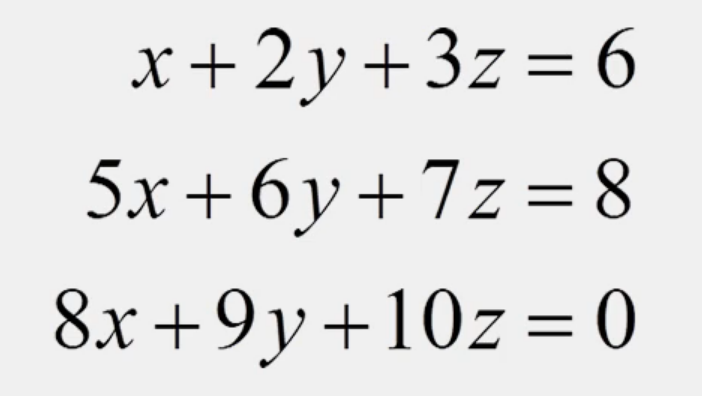
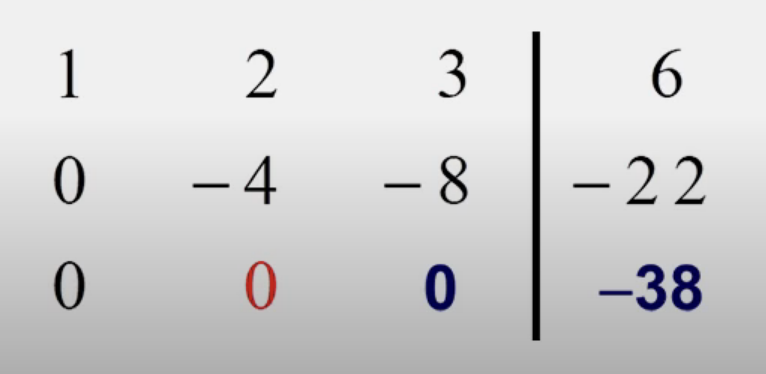
왼쪽 수식을 진행해보면 최종 결과가 오른쪽 사진과 같이 나오게 된다.
0+0+0 = -38 ? 있을 수 없는 식이다. 따라서 해당 방정식은 inconsistent하다는 것을 확인할 수 있다.
inconsistent 여부를 먼저 확인하는 방법은 추후에 소개
++ if consistent and not unique solution
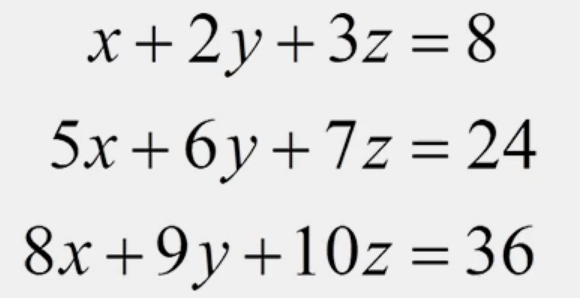
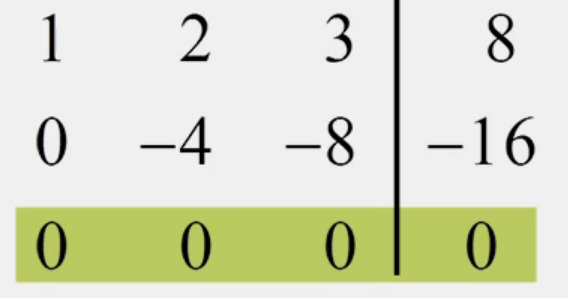
다음도 계산해보면 결론적으로 3개의 변수 x,y,z 와 두개의 방정식이 주어짐을 알 수 있다. 이 경우에는 y=x와 같이 해가 무수히 많은 경우라고 볼 수 있다.(해가 없는 것이 아니다.)
- 이와 같은 예시는 변수가 3개 이므로 좌표상에 표현한다면 하나의 평면이 그려지게 될 것이다.
'AI수학 > Linear Algebra(선형대수학)' 카테고리의 다른 글
| Linear Algebra - Linear combination of vectors (0) | 2023.01.28 |
|---|---|
| Linear Algebraic equation - homogeneous system (0) | 2023.01.27 |
| Linear Algebra - Systems of linear Algebraic equations (0) | 2023.01.27 |
| Linear Algebra(선형대수학) Introduction. (2) | 2023.01.27 |